Электроемкость конденсаторов. Расчет энергии заряженных конденсаторов

Как рассчитать емкость конденсатора по формуле

Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.

Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.

В чем измеряется емкость конденсатора

Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.

Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.

Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.

На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?

Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).

Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.

Полная статья на блоге “Электрик в доме”:

Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.

Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.

Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.

Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.

Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.

• В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.

Формула емкости плоского конденсатора

Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора , рассмотрим формулу для одиночного проводника. Она имеет вид:

• где Q – заряд,
• φ – потенциал.

Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.

Для получения качественного конденсатора важны любые мелочи:

1. ровная поверхность каждой обкладки;
2. обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
3. размеры обкладок должны быть строго идентичными;
4. от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
5. емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.

Теперь обратимся к плоскому конденсатору . Формула определения емкости конденсатора несколько отличается от приведенной выше:

• где S – площадь одной обкладки,
• εr – диэлектрическая проницаемость диэлектрика,
• ε0 – электрическая постоянная,
• d – расстояние между обкладками.

Электрическая постоянная выражается числом 8,854187817×10-12.

Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.

Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.

В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.

Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?

Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.

При уменьшении толщины диэлектрика , а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.

Есть другая формула для плоского переменного конденсатора:

Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.

Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.

Формула емкости цилиндрического конденсатора

Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.

Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:

Задачи на конденсаторы и электроемкость с решениями

Конденсатор – деталька, без которой не обойдется работа ни одного электронного прибора. Но прежде чем разбираться с основами электроники, нужно научиться решать физические задачи на конденсатор и электроемкость. Именно этим мы и займемся в сегодняшней статье, посвященной подробному разбору решений задач.

Подписывайтесь на наш телеграм: теперь помимо полезных и интересных материалов там можно найти скидки и акции на любые работы.

Задачи на конденсаторы и электроемкость с решением

Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.

Задача №1 на электроемкость батареи конденсаторов

Условие

Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?

Решение

Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:

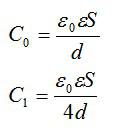
Соединяя 4 таких конденсатора последовательно, получаем:

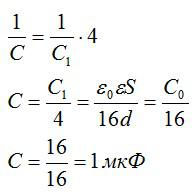
Ответ: 1 мкФ.

Задача №2 на энергию плоского конденсатора

Условие

Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.

Решение

Энергия конденсатора до заполнения диэлектриком равна:

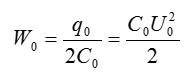
После заполнения емкость конденсатора изменится:

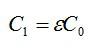
Энергия конденсатора после заполнения:

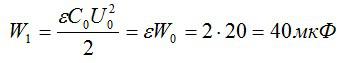
Ответ: 40 мкФ.

Задача №3 на последовательное и параллельное соединение конденсаторов

Условие

На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.

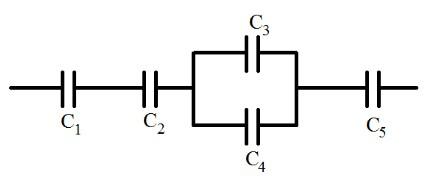
Решение

Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.

Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:

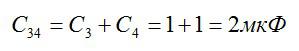
Для последовательного соединения:

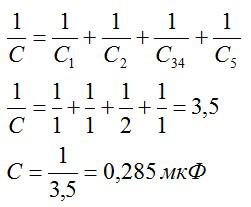
Ответ: 0,285 мкФ.

Задача №4 на пролет частицы в конденсаторе

Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю.

Решение

По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:

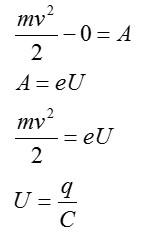
С учетом этого, получим:

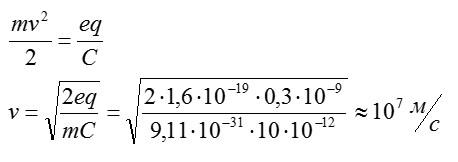
Ответ: 10^7 м/с.

Задача №5 на вычисление энергии электрического поля конденсатора

Условие

Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.

Решение

Заряд конденсатора равен:

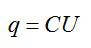
Изменение заряда будет равно:

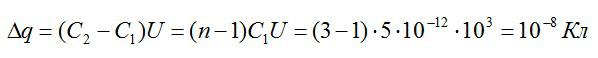
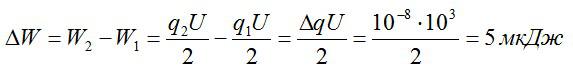
Ответ: 5 мкДж.

Вопросы на тему «Конденсатор и электроемкость»

Вопрос 1. Что такое конденсатор?

Ответ. Конденсатор – устройство, имеющее два полюса и предназначенное для накопления электрического заряда.

Простейший тип конденсатора – плоский воздушный конденсатор. Он состоит из двух пластин (обкладок), имеющих разные заряды и разделенных воздухом. В зависимости от диэлектрика, разделяющего обкладки, разделяют:

• воздушные конденсаторы;
• бумажные конденсаторы;
• слюдяные и другие конденсаторы.

Основная роль конденсатора в электронных приборах – накапливать заряд, а потом передавать его дальше в цепь.

Вопрос 2. Что такое электроемкость?

Ответ. Электроемкость – скалярная физическая величина, характеризующая способность накапливать электрический заряд. В системе СИ измеряется в Фарадах.

Вопрос 3. Какие есть способы соединения конденсаторов?

Ответ. Конденсаторы можно соединить последовательно и параллельно.

При параллельном соединении емкость цепи равна сумме емкостей отдельных конденсаторов.

При последовательном соединении величина, обратная общей емкости, равна сумме обратных емкостей каждого конденсатора.

Вопрос 4. Что такое колебательный контур?

Ответ. Это простейшая электрическая цепь, состоящая из конденсатора, катушки индуктивности и источника тока. В колебательном контуре происходят свободные электромагнитные колебания: энергия конденсатора переходит в энергию катушки, и наоборот.

Вопрос 5. Что происходит при отключении источника питания, к которому подключен конденсатор в цепи?

Ответ. В этот момент конденсатор начинает разряжаться, отдавая накопленный заряд другим элементам цепи.

Мы не понасылшке знаем, что от сложных задач на конденсаторы мозги буквально плавятся. Если ваш мозг устал от постоянного решения задач по физике и других заданий, обращайтесь в профессиональный образовательный сервис за консультацией и поддержкой в любое время. У нас есть решение для ваших проблем с учебой!

Электроемкость. Конденсаторы

Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q 1 и q 2 ), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δ φ . Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U .

В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).

Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника ( q ) к разности потенциалов между этими двумя проводниками.

В виде формулы это записывается так: C = q ∆ φ = q U .

Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф .

Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.

Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.

Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.

Часть электрического поля вблизи конденсатора называется полем рассеяния.

Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.

Рисунок 1 . 6 . 1 . Электрическое поле в плоском конденсаторе.

Рисунок 1 . 6 . 2 . Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.

Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:

Исходя из принципа суперпозиции, можно утверждать, что напряженность E → поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E + → и E – → полей каждой пластины, то есть E → = E + → + E – → .

Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E = 2 E 1 = σ ε 0 .

Как рассчитать электроемкость конденсатора

Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q , а ее площадь как S , то соотношение q S даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками ( d ) , мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.

C = q ∆ φ = σ · S E · d = ε 0 S d .

Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.

Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.

Введем обозначение емкости в виде буквы С и запишем это в виде формулы:

Данная формула называется формулой электроемкости плоского конденсатора.

Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.

Сферическим конденсатором называется система из 2 -х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R 1 и R 2 соответственно.

Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L , а радиусы R 1 и R 2 .

Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:

• C = 4 πε 0 ε R 1 R 2 R 2 – R 1 (сферический конденсатор),
• C = 2 π ε 0 ε L ln R 2 R 1 (цилиндрический конденсатор).

Как рассчитать электроемкость батареи конденсаторов

Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.

Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U 1 = U 2 = U , а заряды можно найти по формулам q 1 = С 1 U и q 2 = C 2 U . При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C , заряд – q = q 1 + q 2 , а напряжение – U . В виде формулы это выглядит так:

С = q 1 + q 2 U или C = C 1 + C 2

Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.

Рисунок 1 . 6 . 3 . Конденсаторы, соединенные параллельно. C = C 1 + C 2

Рисунок 1 . 6 . 4 . Конденсаторы, соединенные последовательно: 1 C = 1 C 1 + 1 C 2

Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q 1 = q 2 = q . Найти их напряжения можно так: U 1 = q C 1 и U 2 = q C 2 . Такую систему тоже можно считать одним конденсатором, заряд которого равен q , а напряжение U = U 1 + U 2 .

C = q U 1 + U 2 или 1 C = 1 C 1 + 1 C 2

Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.

Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.

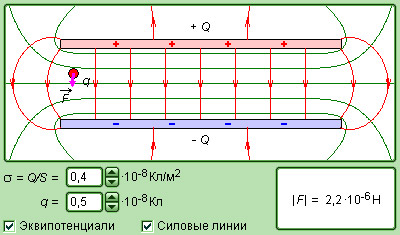
Рисунок 1 . 6 . 5 . Смоделированное электрическое поле плоского конденсатора.

Конденсатор. Энергия электрического поля

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2) :

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Так легче запомнить, не правда ли?

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4) . Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

Соответственно, напряжение на конденсаторе:

Отсюда ёмкость плоского конденсатора с диэлектриком:

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10) : заполнение конденсатора диэлектриком увеличивает его ёмкость.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины d_1)’ alt='(d_2 > d_1)’ /> , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

Это можно переписать следующим образом:

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

Особенно полезными являются формулы (12) и (14) .

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10) .

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Электроемкость конденсатора

Вспышка фотоаппарата и тачскрин на телефоне невозможны без конденсаторов. Да что там — ни один современный прибор без конденсатора работать не будет. Основной параметр конденсатора — электроемкость, о которой мы и поговорим.

· Обновлено 28 октября 2022

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Электроемкость

C = q/φ

С — электроемкость [Ф]

q — электрический заряд [Кл]

φ — потенциал [В]

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух или более проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Зарядка конденсатора — это процесс накопления заряда на двух его обкладках. Заряды на них равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

Электроемкость конденсатора

C = q/U

С — электроемкость [Ф]

q — электрический заряд [Кл]

U — напряжение (разность потенциалов) [В]

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо сквозь диэлектрик. Такой конденсатор больше работать не будет.

Виды конденсаторов

Особенность электроемкости в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости.

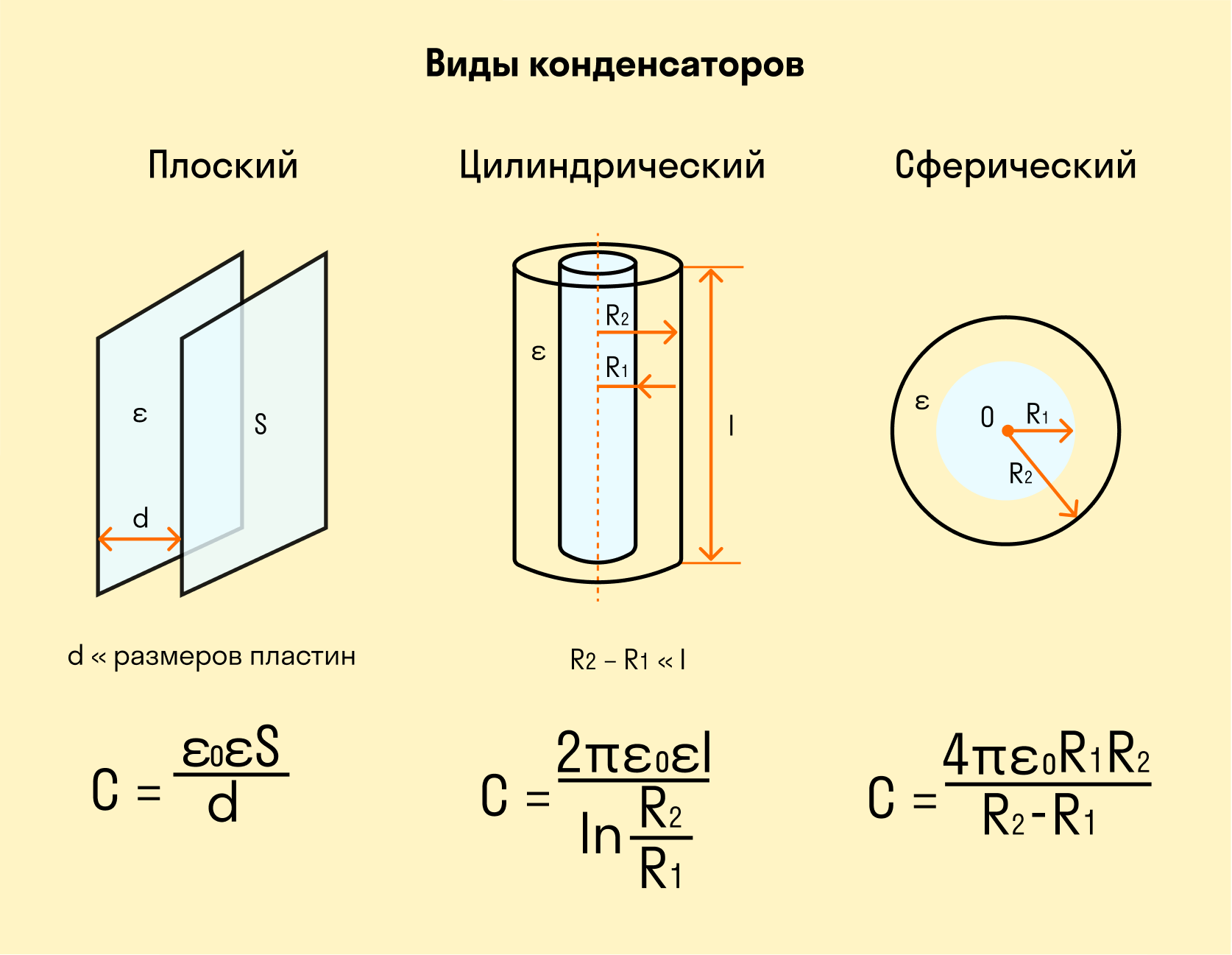
Проще всего вычислить электроемкость плоского конденсатора. Плоский конденсатор состоит из двух металлических пластин, между которыми помещают диэлектрическое вещество.

Электроемкость плоского конденсатора

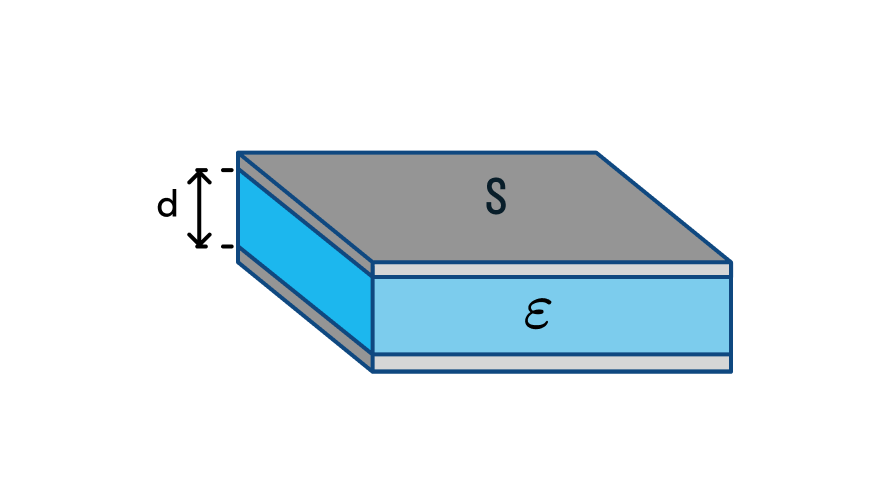
— относительная диэлектрическая проницаемость среды [—]

— площадь пластин [м 2 ]

— расстояние между пластинами [м]

Самый популярный конденсатор — цилиндрический. Он состоит из двух металлических цилиндров, вложенных друг в друга, и диэлектрика, которым заполнено пространство между ними. Рассмотрим формулу электроемкости такого конденсатора.

Электроемкость цилиндрического конденсатора

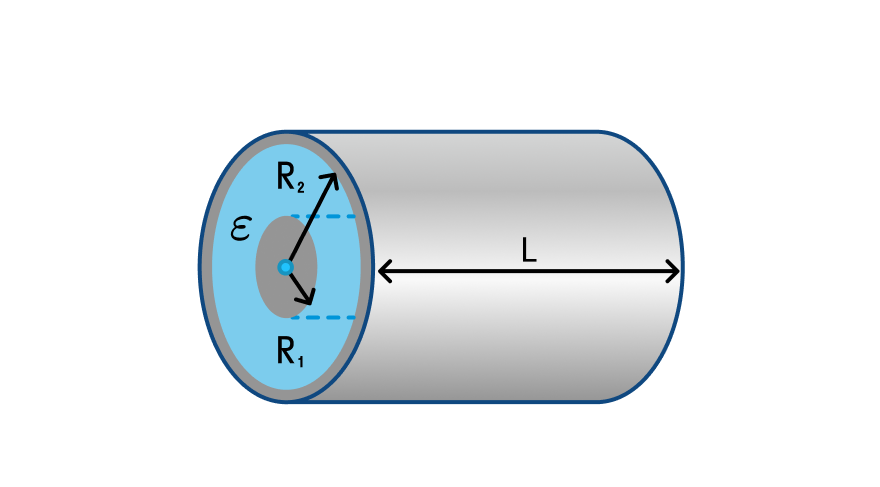
— относительная диэлектрическая проницаемость среды [—]

— длина цилиндров [м]

— радиусы цилиндров [м]

— функция натурального логарифма, которая зависит от радиусов цилиндров

Сферический конденсатор состоит из двух проводящих сфер, вложенных друг в друга, и непроводящей жидкости, которой заполнено пространство между ними.

Электроемкость сферического конденсатора

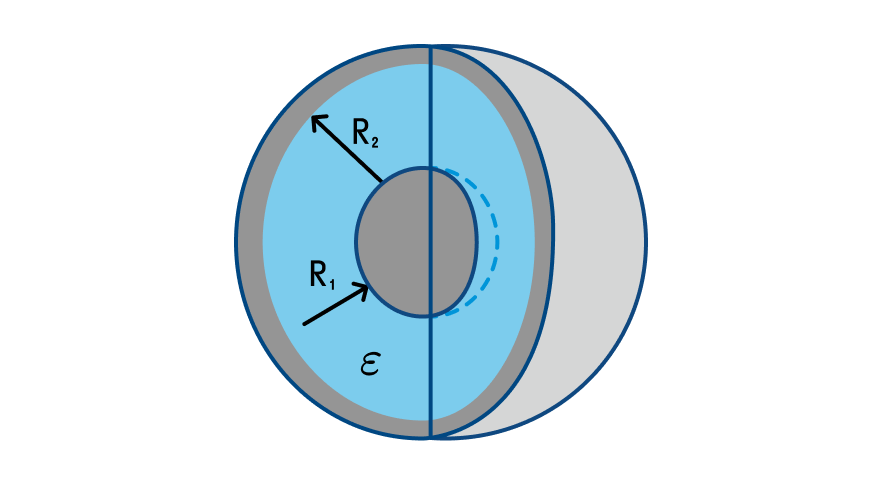
— относительная диэлектрическая проницаемость среды [—]

Подытожим все, что узнали, на картинке-шпаргалке:

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля

W_p = qEd

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

E — напряженность электрического поля [В/м]

d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

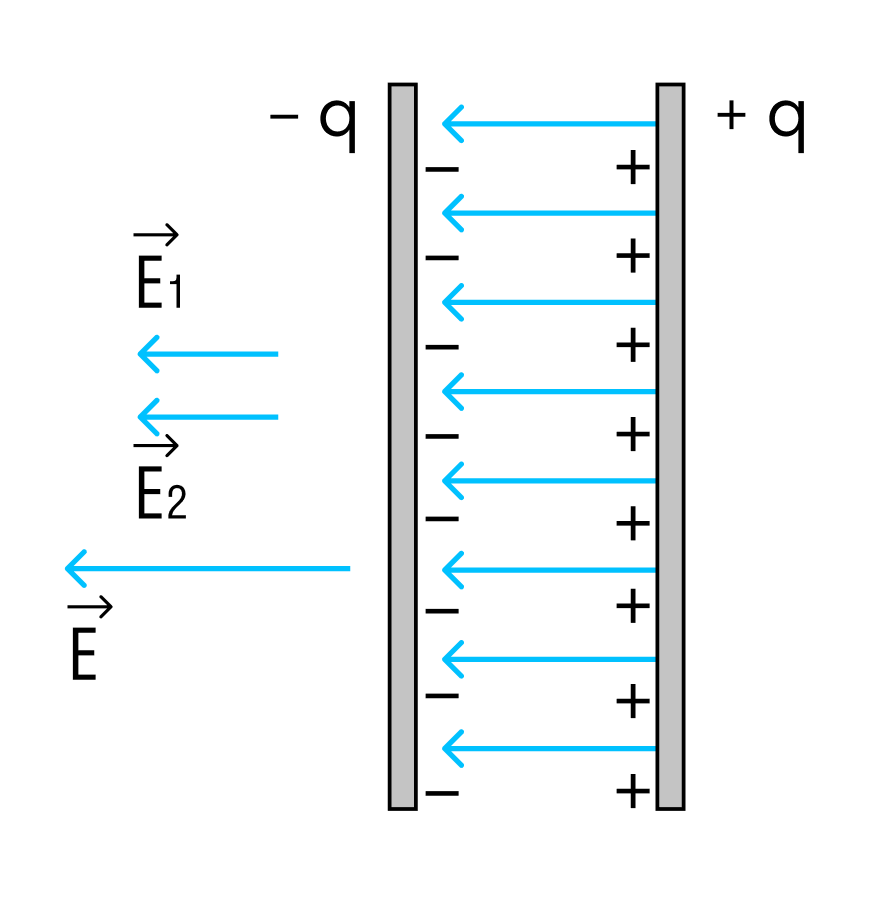
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора

W_p = qU/2

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

U — напряжение на конденсаторе [В]

Энергия конденсатора

W_p = q 2 /2C

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

C — электроемкость конденсатора [Ф]

Энергия конденсатора

W_p = CU 2 /2

W_p — энергия электростатического поля [Дж]

C — электроемкость конденсатора [Ф]

U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Изучать физику на примерах из реальной жизни может быть очень даже интересно. Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.

Конденсаторы

Если тело обладает некоторым электрическим зарядом, то вокруг него обязательно присутствует электрическое поле. Это поле обладает некоторой энергией — может совершить какую-то работу.

Можно ли как-то накопить эту энергию? Да, такая возможность существует. Для этого используют специальный прибор — конденсатор.

Конденсатор — это устройство, позволяющее накапливать электрические заряды и, соответственно, энергию электрического поля.

На данном уроке вы познакомитесь с устройством этого прибора, его характеристиками и свойствами.

Простейший конденсатор и его устройство

Устройство простейшего конденсатора представлено на рисунке 1. Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.

Обкладки расположены на небольшом расстоянии друг от друга. Этот промежуток между ними обязательно должен быть заполнен слоем диэлектрика. В нашем случае таким диэлектриком является обычный воздух.

Такой конденсатор называется плоским (по форме обкладок).

Конденсатор имеет свой условный знак для обозначения на схеме электрической цепи (рисунок 2).

Зарядка конденсатора и его способность накапливать заряды

Теперь разберемся, каким же образом мы можем накапливать заряды с помощью конденсатора.

Рассмотрим простой опыт. Возьмем конденсатор, состоящий из двух металлических пластин, расположенных параллельно друг другу, и заряженный аккумулятор.

Две обкладки конденсатора подключим к разным полюсам аккумулятора. На обкладках начнут образовываться электрические заряды (рисунок 3). Они будут равны друг другу, но иметь противоположные знаки.

Эти заряды образуют электрическое поле конденсатора. Оно будет сосредоточено между обкладками.

Отключим аккумулятор от конденсатора. Что мы увидим? Заряды, образованные на обкладках, никуда не деваются. Они сохраняются, как и электрическое поле между пластин. Конденсатор заряжен.

Если мы соединим проводником обкладки конденсатора, то увидим, что по нему некоторое время будет течь ток. Значит, заряженный конденсатор является источником тока в электрической цепи.

Электроемкость конденсатора

Логично предположить, что разные конденсаторы по-разному будут накапливать заряд. Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.

Чтобы понять смысл этой величины, рассмотрим опыт. Возьмем две металлические пластины и установим их на изолированных подставках друг напротив друга.

Подключим к пластинам электрометр. Этот прибор (рисунок 4) по своему устройству и принципу действия схож с электроскопом. Он позволит нам зафиксировать значения напряжения, которое возникнет между пластинами.

Итак, одну из пластин (A) мы соединим проводом со стержнем электрометра, а другую (B) соединим с корпусом прибора (заземлим). Коснемся положительно наэлектризованной стеклянной палочкой внешней стороны пластины A (рисунок 5).

Мы сообщили пластине A положительный заряд $+q$. Вокруг этого заряда (пластины A) теперь существует электрическое поле. Под его действием произойдет перераспределение зарядов в пластине B. Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.

Помните, что мы заземлили пластину B? За счет этого на пластину пойдут свободные электроны с земли. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, мы получили на пластине B отрицательный заряд $-q$ (рисунок 6). По величине он равен заряду на другой пластине.

Стрелка электрометра отклонилась. Зафиксируем это значение напряжения между пластинами. Далее мы снова сообщим заряд пластине B, равный по величине первому сообщаемому заряду. Потом сообщим третий и четвертый такие же заряды, наблюдая за стрелкой электрометра.

Вы увидите, что при увеличении заряда в 2, 3, 4 раза, соответственно, в 2, 3, 4 раза увеличиваются показания электрометра — напряжение между пластинами. Важно отметить, что отношение заряда к напряжению при этом будет постоянно:
$frac = frac = frac = frac = const$.

Теперь мы можем дать определение электроемкости конденсатора.

Электроемкость конденсатора — это величина, измеряемая отношением заряда на одной из пластин конденсатора к напряжению между пластинами:
$C = frac$.

Единицы измерения электроемкости

В СИ электроемкость измеряется в фарадах ($Ф$).

Электроемкость конденсатора равна единице, если при сообщении ему заряда в $1 space Кл$ возникает напряжение, равное $1 space В$ (рисунок 7):
$1 space Ф = frac$.

Эта единица измерения названа в честь английского физика Майкла Фарадея (рисунок 8).

Рисунок 8. Майкл Фарадей (1791-1867) — английский физик-экспериментатор

Емкость в $1 space Ф$ является очень большой, поэтому на практике часто используют дольные единицы: микрофарад ($мкФ$) и пикофарад ($пФ$).

Зависимость электроемкости от площади пластин конденсатора

От чего зависит электроемкость? Начнем с размера пластин.

Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).

Мы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).

Из определения электроемкости:
$C_1 = frac$,
$C_2 = frac$,
$C_2 > C_1$.

Чем больше площадь пластин, тем больше электроемкость конденсатора.

Зависимость электроемкости от расстояния между пластинами конденсатора

Снова обратимся к опыту. Теперь изменим расстояние между пластинами — уменьшим его (рисунок 10).

Мы увидим, что напряжение между пластинами уменьшилось: $U_2 < U_1$. Значит,
$C_1 = frac$,
$C_2 = frac$,
$C_2 > C_1$.

При уменьшении расстояния между пластинами конденсатора и при неизменном заряде электроемкость конденсатора увеличивается.

Зависимость электроемкости от диэлектрика

Проведем еще один опыт. Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.

Если раньше диэлектриком между пластинами являлся только воздух, то теперь это и воздух, и лист оргстекла. Напряжение между пластинами уменьшилось: $U_1 > U_2$. Значит,
$C_1 = frac$,
$C_2 = frac$,
$C_2 > C_1$.

При внесении диэлектрика электроемкость конденсатора увеличивается.

Виды конденсаторов

Между обкладками конденсатора могут быть помещены разнообразные диэлектрики. В зависимости от природы этого диэлектрика конденсаторы разделяют на несколько видов: с твердым, жидким и газообразным диэлектриком.

Также существует классификация и по форме обкладок. Конденсаторы бывают плоские, цилиндрические, сферические (рисунок 12) и др.

Конденсаторы бывают с постоянной емкостью и с переменной емкостью. В последних можно регулировать параметры, от которых зависит емкость — ширину пластин и расстояние между ними.

На данный момент существует огромное разнообразие конденсаторов (рисунок 13). Многие из них носят названия, происходящие от названий материалов, составляющих их: слюдяные, керамические, алюминиевые электролитические, танталовые электролитические, конденсаторы на полимерной пленке.

Рисунок 13. Современные конденсаторы

Энергия конденсатора и работа его электрического поля

Заряженный конденсатор обладает некоторой энергией. Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.

Откуда взялась эта энергия? Конденсатор получает ее при зарядке.

Для того, чтобы зарядить конденсатор, нужно совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии совершенная работа A и будет равна энергии конденсатора E:
$A = E$.

Для расчета такой работы электрического поля конденсатора существует специальная формула.

В процессе разрядки напряжение постоянно падает, поэтому нам и необходимо знать для расчетов его среднее значение:
$U_ = frac$.

Из формулы для электроемкости:
$C = frac$,
$q = CU$.

Подставим в формулу для работы:
$A = frac = frac = frac$.

По закону сохранения энергия эта работа и будет равна энергии конденсатора $W$.

Накапливание конденсатором энергии часто происходит достаточно длительное время. При разрядке эта энергия отдается почти мгновенно.

Это свойство (накопление энергии и ее быстрая отдача) широко применяется в различных электронных устройствах, в медицинской технике (рентген, устройства для электротерапии), при изготовлении дозиметров, фотосъемке.

Последовательное соединение конденсаторов

В электрической цепи может быть не один, а сразу несколько конденсаторов. Они могут быть соединены как последовательно, так и параллельно.

Рассмотрим первый тип соединения — последовательный (рисунок 15).

Обкладки 2 и 3, принадлежащие разным конденсаторам, будут являться отдельной деталью. По закону сохранения заряда, заряды на обкладках 2 и 3 будут равны друг другу по модулю, но противоположны по знаку. Из этого следует, что общий заряд конденсаторов численно будет равен заряду на любой из обкладок конденсаторов.

Напряжение на концах участка цепи с последовательно соединенными конденсаторами будет складываться из значения напряжений на каждом конденсаторе.

Чтобы получить формулу для общей емкости конденсаторов, последнее равенство нужно разделить на заряд q (любой, так как они равны).

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов показано на рисунке 16.

В этом случае выходы от источника питания будут соединены с каждой обкладкой конденсаторов. Поэтому напряжение на концах такого участка цепи будет равно напряжению между обкладками любого из конденсаторов.

Заряды на обкладках будут суммироваться.

Разделим это равенство на значение напряжения и получим формулу для электроемкости параллельно соединенных конденсаторов.

$C = C_1 + C_2 + … + C_n$

Первый конденсатор — лейденская банка

Лейденская банка официально является первым конденсатором. Изобретение ее относится к 1745 году. Существует множество версий о том, кто же именно должен считаться изобретателем этого прибора, но официально авторство принадлежит Питеру ван Мушенбруку и его студенту Андреасу Кунэусу.

В ранней версии лейденская банка была на часть заполнена водой, которая выступала в роли обкладки (рисунок 17). Второй обкладкой являлась рука, держащая банку. После зарядки этого приспособления Андреас Кунэус испытал сильный удар током, коснувшись до верха металлического стержня.

Более поздняя и более распространенная версия этого незамысловатого прибора представляет собой сосуд из стекла с широким горлом, снаружи покрытый листом из фольги (рисунок 18). Фольга также находится и внутри банки. Через пробку в этот сосуд вставляется металлический стержень. Он должен касаться фольги внутри банки.

Таким образом, фольга внутри и фольга снаружи становятся своеобразными обкладками. При подключении к источнику тока на них накапливается электрический заряд.

Внимание! Лейденская банка не является безопасным инструментом в электротехнике! Разряд такого конденсатора может оказаться смертельным или привести к серьезным физическим повреждениям. Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.

Как изготовить лейденскую банку своими руками? Возьмите пластиковую банку с крышкой (из-под кофе, витаминов). Внешнюю сторону банки на $frac$ обклейте фольгой. Далее или налейте в банку соленую воду, или обклейте изнутри фольгой. Затем закройте крышку и проткните ее достаточно длинным гвоздем, чтобы он касался внутренней обкладки (воды или фольги). После зарядки такая банка представляет собой заряженный конденсатор.

Упражнения

Упражнение №1

Пластины плоского конденсатора подсоединяют к источнику напряжения в $220 space В$. Емкость конденсатора равна $1.5 cdot 10^ space мкФ$. Чему будет равен заряд конденсатора?

Дано:
$C = 1.5 cdot 10^ space мкФ$
$U = 220 space В$

СИ:
$С = 1.5 cdot 10^ space Ф$

Посмотреть решение и ответ

Решение:

Формула для расчета электроемкости конденсатора:
$C = frac$.

Выразим отсюда заряд конденсатора и рассчитаем его:
$q = CU$,
$q = 1.5 cdot 10^ space Ф cdot 220 space В = 33 cdot 10^ space Кл$.

Ответ: $q = 33 cdot 10^ space Кл$.

Упражнение №2

Заряд плоского конденсатора равен $2.7 cdot 10^ space Кл$, его емкость составляет $0.01 space мкФ$. Найдите напряжение между обкладками конденсатора.

Дано:
$C = 0.01 space мкФ$
$q = 2.7 cdot 10^ space Кл$

СИ:
$C = 10^ space Ф$

Показать решение и ответ

Решение:

Формула для расчета электроемкости конденсатора:
$C = frac$.

Выразим отсюда напряжение между обкладками конденсатора и рассчитаем его:
$U = frac$,
$U = frac space Кл> space Ф> = 2.7 cdot 10^6 space В$.

Конденсаторы. Электроемкость конденсатора. Энергия заряженного конденсатора. Применение конденсаторов

Электроемкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между этим проводником и соседним.

Электроемкость двух проводников равна единице, если при сообщении им зарядов ±1 Кл между ними возникает разность потенциалов 1 В. Эту единицу называют фарад (Ф); 1 Ф=1 Кл/В.

Конденсатор – это временный источник тока. Они имеют одно и свойство: конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используются широко на практике

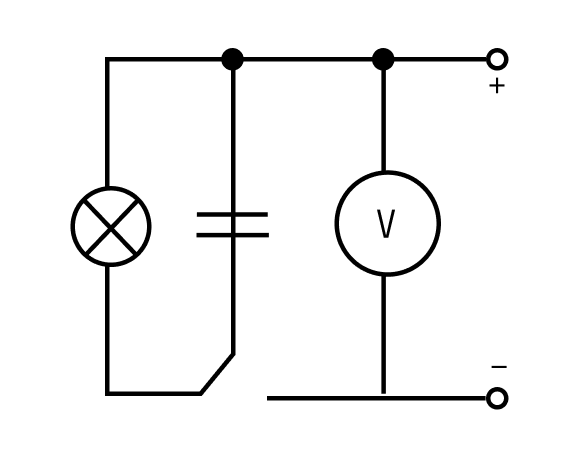
Конденсатор обладает энергией: . Это можно доказать следующим опытом.

Рассмотрим цепь (рис1): при замыкании цепи в положение 1 конденсатор заряжается. При замыкании цепи в положение 2 конденсатор мгновенно отдает энергию – мы видим, что лампочка загорается и гаснет. Это доказывает, что конденсатор обладает энергией.

Конденсаторы применяются для накопления электроэнергии и использования её при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного токов, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах.
14/2. Качественные задачи по теме «Строение атома. Фотоэффект».

Почему происходит фотоэффект при облучении металла слабым ультрафиолетовым излучением и не происходит при облучении инфракрасным излучением любой интенсивности?

ОТВЕТ. См.билет 23/1 – красная граница фотоэффекта.

Работа и мощность в цепи постоянного тока. Электродвижущая сила. Закон Ома для полной цепи.

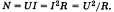
Мощность по определению N = A/t, следовательно,

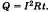
Русский ученый X. Ленд и английский ученый Д. Джоуль опытным путем в середине прошлого века установили независимо друг от друга закон, который называется законом Джоуля — Ленца и читается так: при прохождении тока по проводнику количество теплоты, выделившееся в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. .

Полная замкнутая цепь представляет собой электрическую цепь, в состав которой входят внешние сопротивления и источ-ник тока (рис. 25). Как один из участков цепи, источник тока обладает сопротивлением, которое

называют внутренним, r.

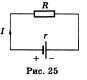
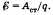
Для того чтобы ток проходил по замкнутой цепи, необходимо, чтобы в источнике тока зарядам сообщалась дополнительная энергия, она появляется за счет работы по перемещению зарядов, которую производят силы неэлектрического происхождения (сторонние силы) против сил электрического поля. Источник тока характеризуется энергетической характеристикой, которая называется ЭДС — электродвижущая сила источника. ЭДС измеряется отношением работы сторонних сил по перемещению вдоль замкнутой цепи положительного заряда к величине этого заряда

тивление участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи. Обычно это выражение записывают так: I = E/(R + г). Эту зависимость опытным путем получил Георг Ом, называется она законом Ома для полной цепи и читается так: сила тока в полной цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи. При разомкнутой цепи ЭДС равна напряжению на зажимах источника и, следовательно, может быть измерена вольтметром
15/2. Качественные задачи по теме «Элементы астрофизики».

Что является источником энергии звезд?

ОТВЕТ. Реакции термоядерного синтеза – см. билет 24.1.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: